1. 前言

模型：

ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。

而SARIMAX是在ARIMA的基础上加上季节（S, Seasonal）和外部因素(X, eXogenous)。也就是说以ARIMA基础加上周期性和季节性，适用于时间序列中带有明显周期性和季节性特征的数据。

ARIMA是一个非常强大的时间序列预测模型，但是数据准备与参数调整过程非常耗时，Auto ARIMA让整个任务变得非常简单，舍去了序列平稳化，确定d值，创建ACF值和PACF图，确定p值和q值的过程

目的：
本文的目的是分别使用ARIMA、SARIMAX与Auto ARIMA来预测未来一年的汽车月销量。

工具：
语言：Python 3.8
软件：Jupyter Notebook，Pycharm
库：pandas、numpy、matplotlib、requests、statsmodels、pmdarima等

2. 爬虫

搜狐汽车的web网页(点击链接)含有过去十几年的国内乘用车的月度销量数据。
如图：

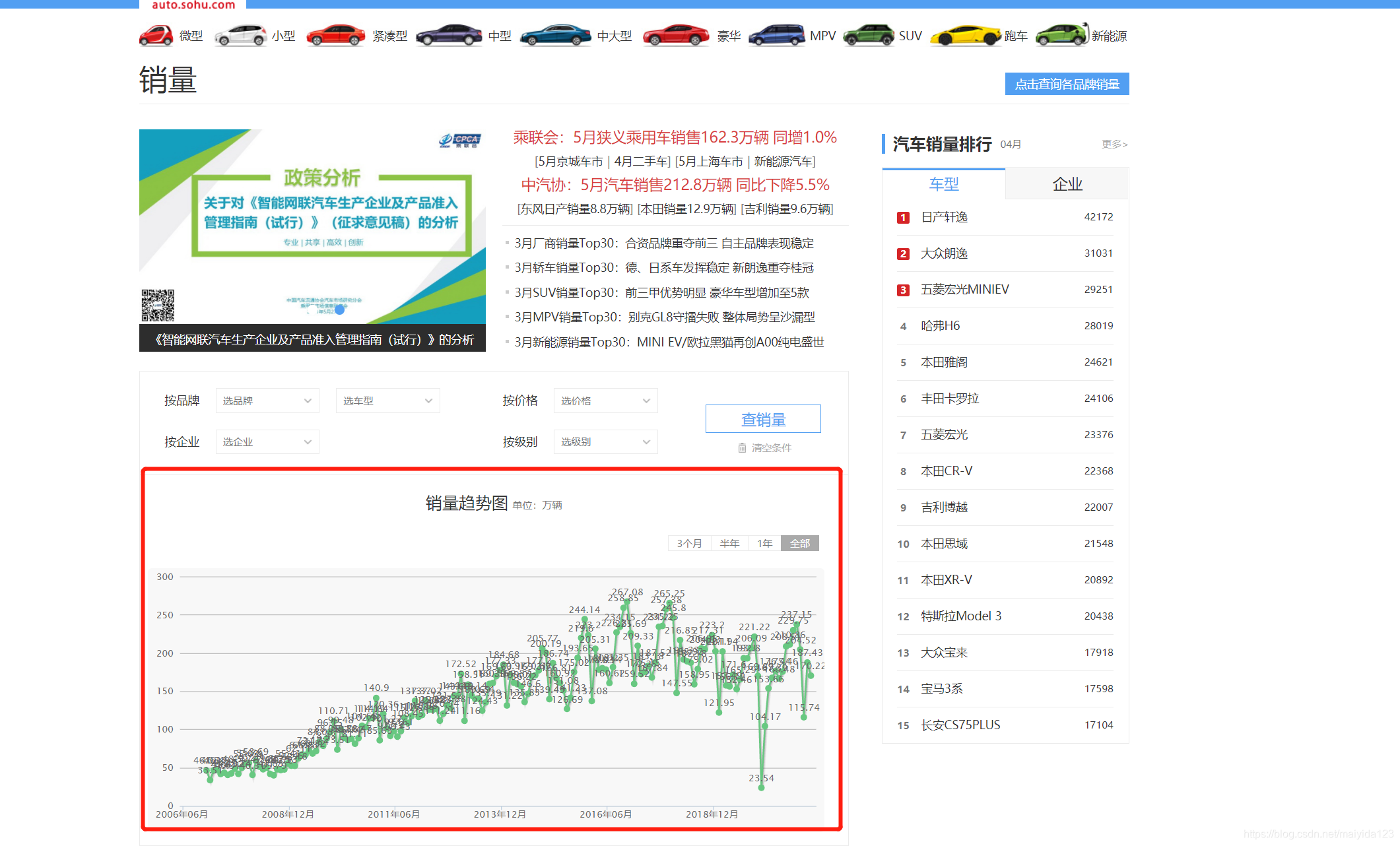
利用键盘 F12 打开调试页面，第一步点击 XHR，第二步点击图表中的 全部， 第三步点击出现的事件 total?section = 0，便可以看到出现右侧以下的页面，这里的headers便是我们想要的获取的请求头信息，圈出的url便是请求的url。

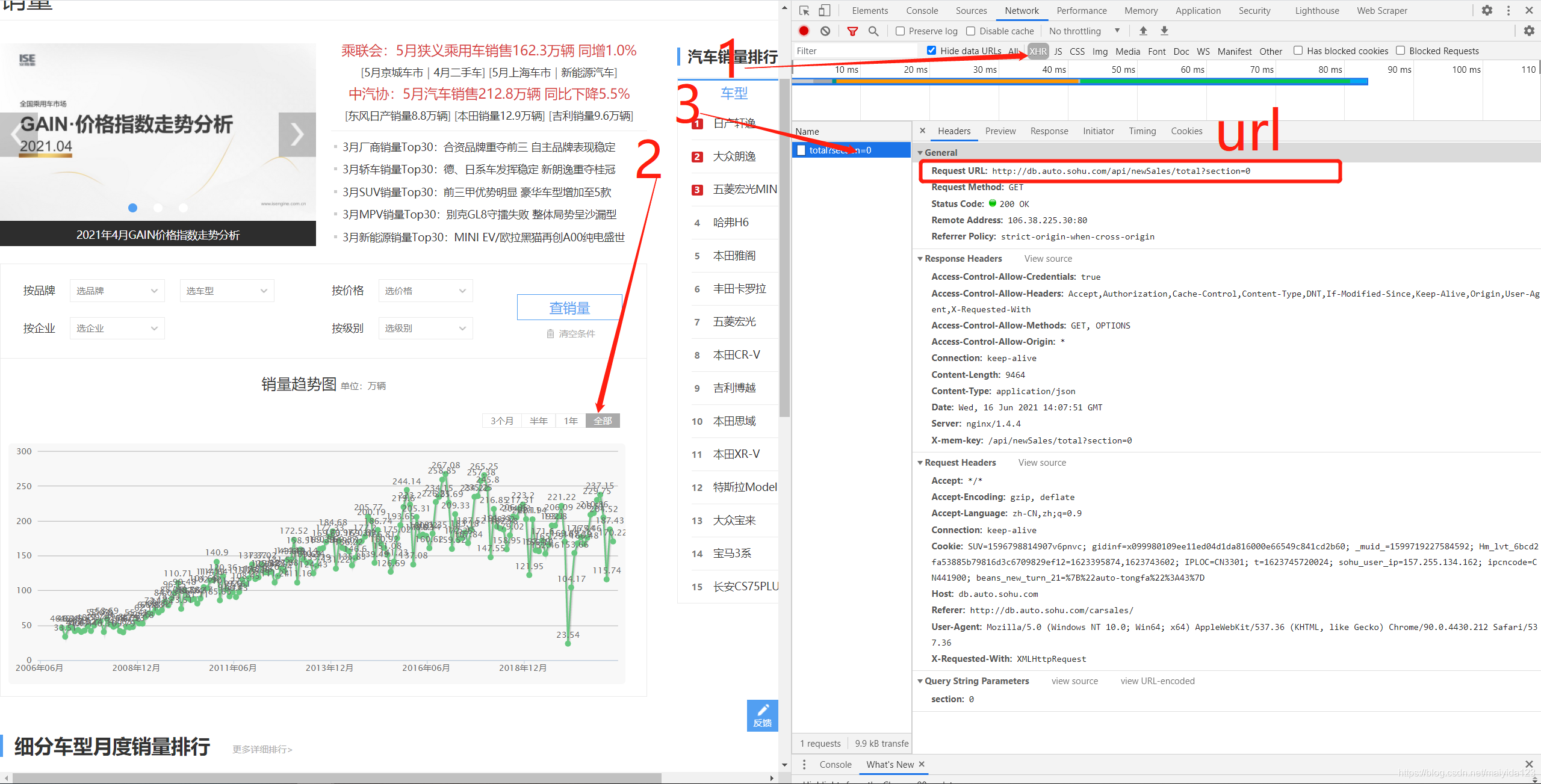
进一步点击preview预览响应内容，并依次点开下一级，可以看到我们想要获取的汽车销量数据。

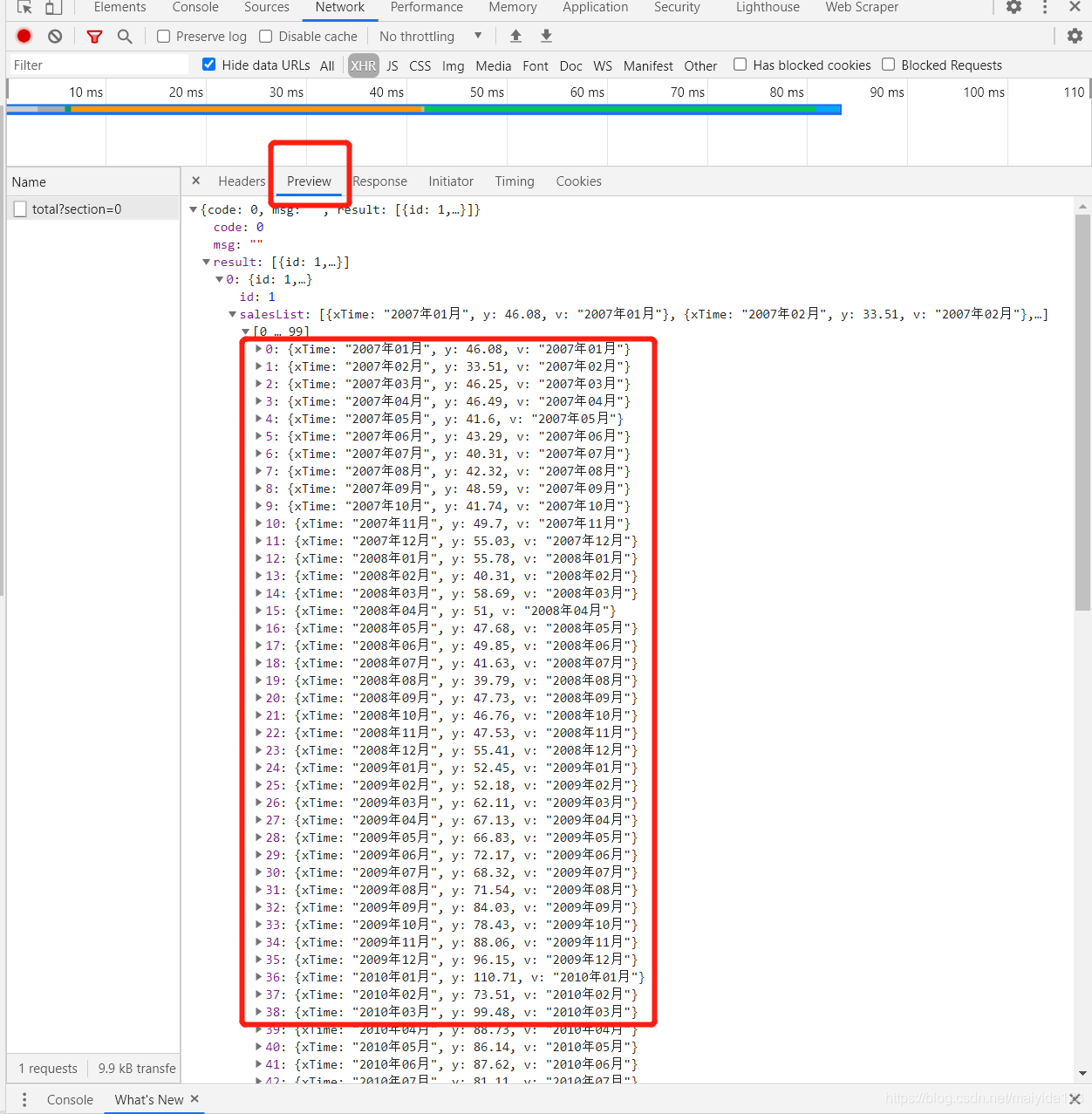
爬取代码：

import requests
import pandas as pd

headers = {
    
	'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/88.0.4324.104 Safari/537.36',
	}

url = 'http://db.auto.sohu.com/api/newSales/total?section=0'
response = requests.get(url,  headers = headers)

df = pd.DataFrame([[i['v'],i['y']] for i in response.json()['result'][0]['salesList']], 
                  columns = ['date', 'sales']).set_index('date')

df

• 从上可以看到一共获取了172行数据，爬虫工作完毕。

3. ARIMA

ARIMA模型的通用步骤如下：

1. 加载数据：构建模型的第一步为加载数据集。
2. 预处理：根据数据集定义预处理步骤。包括创建时间戳、日期/时间列转换为d类型、序列单变量化等。
3. 序列平稳化：为了满足假设，应确保序列平稳。这包括检查序列的平稳性和执行所需的转换。
4. 确定d值：为了使序列平稳，执行差分操作的次数将确定为d值。
5. 创建ACF和PACF图：这是ARIMA实现中最重要的一步。用ACF PACF图来确定ARIMA模型的输入参数。
6. 确定p值和q值：从上一步的ACF和PACF图中读取p和q的值。
7. 拟合ARIMA模型：利用我们从前面步骤中计算出来的数据和参数值，拟合ARIMA模型。
8. 在验证集上进行预测：预测未来的值。
9. 计算RMSE：通过检查RMSE值来检查模型的性能，用验证集上的预测值和实际值检查RMSE值。

3.1 数据清洗

导入所需要的库

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.style.use('fivethirtyeight')
import warnings
warnings.filterwarnings("ignore")

由于只爬取到4月份的数据，现在是6月中旬，5月的销量数据网站还没更新，所以我们手动添加查到的5月销量数据。

# 添加2021年5月的数据
df = df.append(pd.DataFrame([164.6], index = ['2021年05月'], columns =['sales']))

查看缺失值

# 查看缺失值---没有缺失值
df.isnull().sum()

• 没有缺失值

查看时序图

# 查看时序分布图
plt.figure(figsize=(12, 5)) 
df.sales.plot(rot = 30)
plt.show()

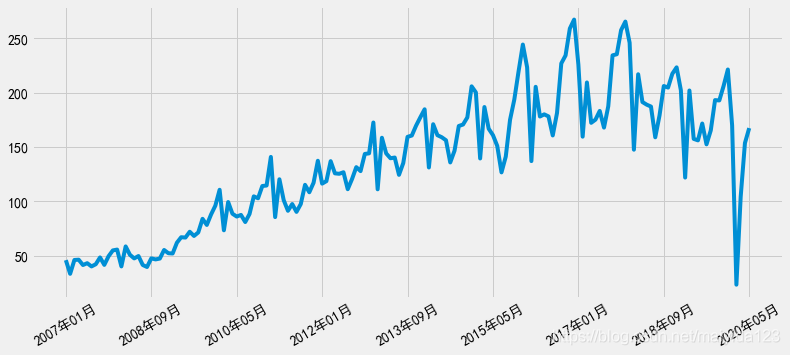
观察时序图可知：

1. 存在趋势性与季节性，初步判断数据是非平稳的时间序列。
2. 波幅大小有变化，对原数据进行对数处理。
3. 2020年2,3月因为新冠疫情的影响，汽车销量暴跌，这里将其视作异常值处理

异常值处理

# 异常值处理
from sklearn.linear_model import LinearRegression
x = [[i] for i in np.arange(1,4)]
y = df.loc[['2017年02月','2018年02月', '2019年02月'], 'sales'].values
y1 = df.loc[['2017年03月','2018年03月', '2019年03月'], 'sales'].values
LR_model = LinearRegression().fit(x, y)
LR_model1 = LinearRegression().fit(x, y1)
df.loc['2020年02月', 'sales'] = LR_model.predict([[4]])
df.loc['2020年03月', 'sales'] = LR_model1.predict([[4]])

• 这里利用线性回归拟合2020年之前的3个不同年份相同月份的数据，来预测2020年的该月的销量

index转换为dateindex格式

# 将index转换为时间格式
df.index = pd.to_datetime(df.index.str.replace("年","-").str.replace("月", ""))
# 再将index转换为DatetimeIndex
df.index = pd.DatetimeIndex(df.index.values, freq = df.index.inferred_freq)

划分测试集与验证集

# 划分测试集与验证集
df_train = df.iloc[:-12, ]
df_test = df.iloc[-12:, ]

• 选择最近的12个月为验证集

至此，数据清洗完毕，接下来进行分析。

3. 2 数据分析

3.2.1 周期性

seasonal_decompose函数可以分解时间序列，提取序列的趋势、季节和随机效应。

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(df_train.sales, model='multiplicative')
fig = plt.figure()
fig = decomposition.plot()
fig.set_size_inches(15,12)
plt.show()

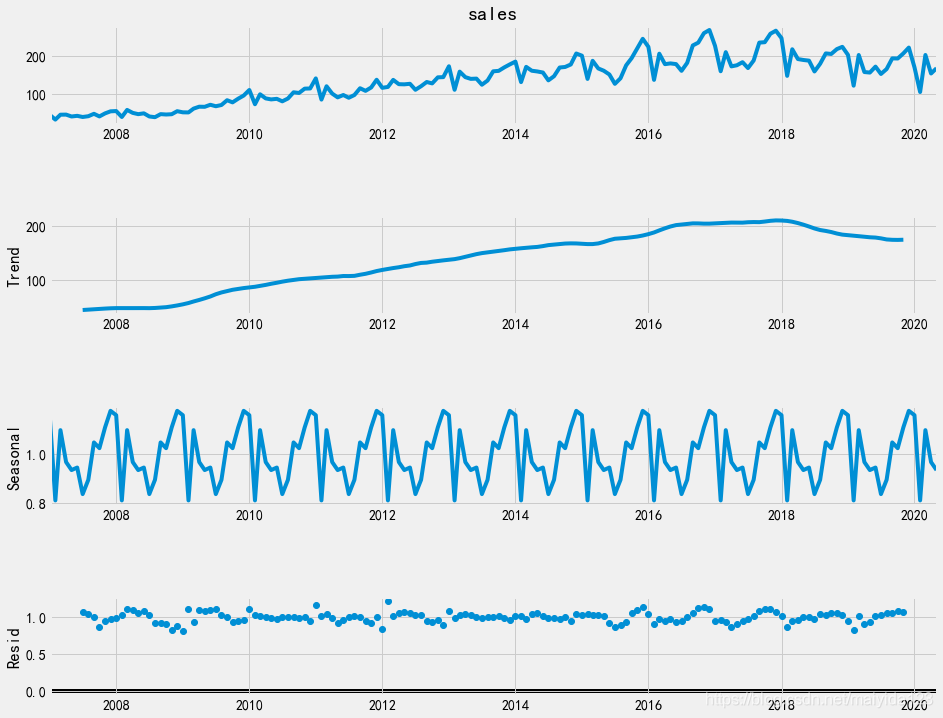
由图可得：

• 乘用车销售量整体呈现上升的趋势，在18年达到峰值后有逐渐的下降趋势；
• 序列具有周期长度为12个月的季节变动；
• 序列的残差基本稳定。

3.2.2 平稳性

3.2.2.1 对数变换

1. 当原序列的前后数值相差较大或者数量级相差较大时，一般取对数将指数趋势转化为线性趋势，而且还不会改变变量之间的统计性质，同时得到较平稳的序列。
2. 观察时序图可知波幅有先增大后减小趋势，所以我们对原数据取对数。

# 对数变换
df_train['sales_ln'] = np.log(df_train.sales)
# 查看时序图
plt.figure(figsize=(12, 5)) 
df_train.sales_ln.plot()
plt.show()

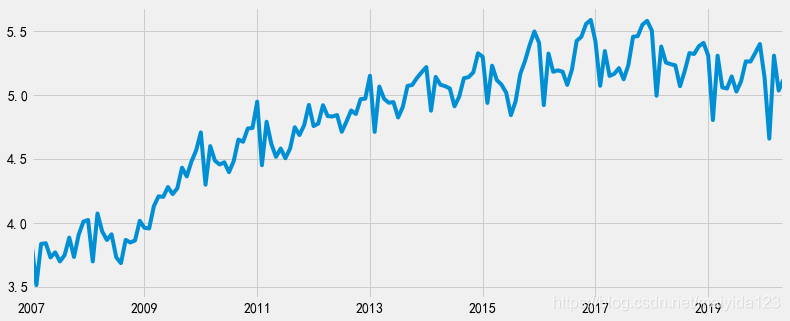
• 与原序列相比，对数变换后的时间序列的波幅基本一致了，仍然存在趋势性与季节性

3.2.2.2 差分

非平稳序列可以通过差分来消除趋势性，得到平稳序列。

一阶差分

# 取一阶差分
df_train['sales_ln_diff1'] = df_train.sales_ln.diff(periods=1)
df_train.dropna(subset=['sales_ln_diff1'], inplace=True)
# 查看差分之后的时序图
plt.figure(figsize=(12, 5)) 
df_train.sales_ln_diff1.plot()
plt.show()

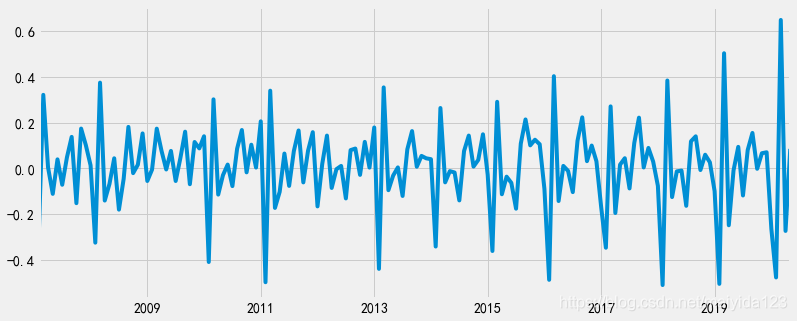
• 一阶差分后，看似时序图显示序列转化为了平稳时间序列，但仍具有周期性

二阶差分

# 二阶差分，取步长为12
df_train['sales_ln_diff12'] = df_train.sales_ln_diff1.diff(periods=12)
df_train.sales_ln_diff12.dropna(inplace=True)
# 查看差分后的时序图
plt.figure(figsize=(12, 5)) 
df_train.sales_ln_diff12.plot()
plt.show()

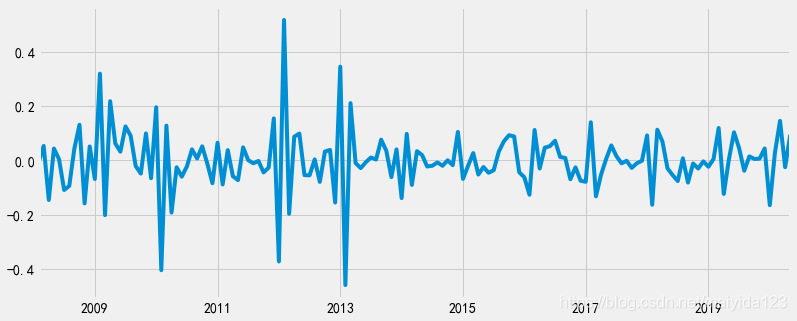
• 经过两次差分（即一阶12步差分）之后，时序图可以发现，移动平均值在0值上下波动，且方差随着时间的变化波动也非常小，这说明差分后的序列近似平稳。

3.2.2.3 平稳性检验

检验序列平稳性的常用方法是ADF检验。其零假设为时间序列是非平稳的。

from statsmodels.tsa.stattools import adfuller as adf
print('adfuller test p-value：', adf(df_train.sales_ln_diff12)[1])

结果：

• adfuller test p-value： 1.6247501437375345e-05
• 根据ADF检验结果可知，p值小于0.05。所以可以拒绝原假设，认为两次差分之后的序列是平稳的。

3.2.2.4 白噪声检验

LB 检验是时间序列分析中检验序列自相关性的方法。用来检验m阶滞后范围内序列的自相关性是否显著，或序列是否为白噪声。其原假设为序列是白噪声序列。

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print('LB test p-value：', acorr_ljungbox(df_train.sales_ln_diff12, lags=1)[1][0])

结果：

• LB test p-value： 2.2197814055368676e-12
• p值小于0.05，拒绝原假设，所以二阶差分之后的序列是平稳非白噪声序列

3.3 定阶

3.3.1 看图定阶

# 查看自相关系数与偏相关系数
from statsmodels.graphics.tsaplots import plot_pacf, plot_acf
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
plot_acf(df_train.sales_ln_diff12, ax=ax[0]).show()
plot_pacf(df_train.sales_ln_diff12, ax=ax[1]).show()

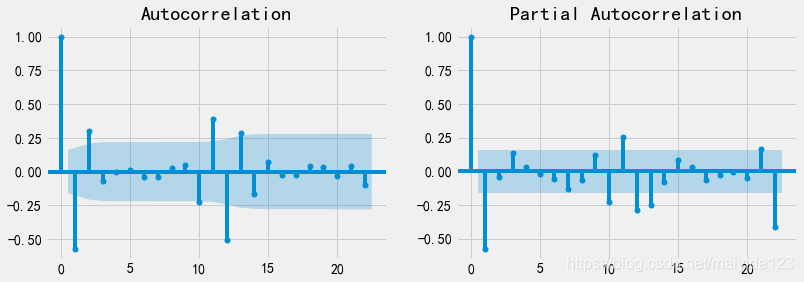
• 从上图可得，ACF为二阶拖尾，PACF为一阶拖尾。

平稳时间序列的识别方法如下图，所以选择ARMA(2, 1)模型。

3.3.2 参数遍历

通过看图判断具有一定的主观性，通过遍历可能的参数选择AIC/BIC统计量最小的模型相对更适合

%%time
p_max = q_max = np.arange(6)
aic_matrix = []  # AIC矩阵
bic_matrix = []  # BIC矩阵
for p in p_max:
    aic_tmp, bic_tmp = [], []
    for q in q_max:
        try:  # 存在部分报错，所以用try来跳过报错。
            mod = sm.tsa.ARMA(df_train.sales_ln_diff12, (p, q)).fit()
            aic_tmp.append(mod.aic)
            bic_tmp.append(mod.bic)
        except:
            aic_tmp.append(None)
            bic_tmp.append(None)
    
    aic_matrix.append(aic_tmp)
    bic_matrix.append(bic_tmp)

分别选择AIC 、BIC最小的pq值建模

aic_df, bic_df  = pd.DataFrame(aic_matrix),  pd.DataFrame(bic_matrix)
aic_p, aic_q = aic_df.stack().idxmin()
bic_p, bic_q = bic_df.stack().idxmin()
print('AIC最小的 p = %s  q = %s' %(aic_p, aic_q)) 
print('BIC最小的 p = %s  q = %s' %(bic_p, bic_q)) 

结果：

• AIC最小的 p = 3 q = 5
• BIC最小的 p = 2 q = 1
• 可以看到BIC最小的结果与看图定阶的结果一致。

3.4 建模

import statsmodels.api as sm
arma_aic = sm.tsa.ARMA(df_train.sales_ln_diff12, (aic_p, aic_q)).fit()
arma_bic = sm.tsa.ARMA(df_train.sales_ln_diff12, (bic_p, bic_q)).fit()

# 定义一个一阶12步差分还原函数
def diff_restore(arma):
    date_index = pd.date_range(start='2020-06-01', periods=24, freq='MS')
    arma_pred = arma.forecast(steps=24)[0]  # 预测未来24个月
    diff1_pred12 = pd.Series(df_train.sales_ln_diff1[-12:].values - arma_pred[:12], index = date_index[:12])
    diff1_pred24 = diff1_pred12.append(pd.Series(diff1_pred12.values - arma_pred[12:], index = date_index[12:]))  # 二阶差分还原
    sales_ln_pred = pd.Series([df_train.sales_ln[-1]], index=[df_train.index[-1]]).append(diff1_pred24).cumsum()[1:]  # 一阶差分还原
    sales_pred = np.power(np.e, sales_ln_pred)  # 因为取对数之后进行的差分操作，所以需要取自然底数还原
    return sales_pred

sales_pred_aic = diff_restore(arma_aic)
sales_pred_bic = diff_restore(arma_bic)

# 模型评估---rmse
print('AIC预测值的rmse为 %.2f'%np.sqrt(((sales_pred_aic[:12].values - df_test.sales.values) ** 2).mean()))
print('BIC预测值的rmse为 %.2f'%np.sqrt(((sales_pred_bic[:12].values - df_test.sales.values) ** 2).mean()))

结果：

• AIC预测值的rmse为 24.17
• BIC预测值的rmse为 15.00

通过比较rmse值，可知验证集上BIC的效果更好，所以我们使用BIC最小的模型。

3.5 诊断

# 检验
import scipy.stats as stats

fig = plt.figure(figsize=(16,12))
layout = (2, 2)
ts_ax   = plt.subplot2grid(layout, (0, 0))
hist_ax = plt.subplot2grid(layout, (0, 1))
qq_ax = plt.subplot2grid(layout, (1, 0))
acf_ax = plt.subplot2grid(layout, (1, 1))

arma_bic.resid.plot(ax=ts_ax) # 折线图
arma_bic.resid.plot(ax=hist_ax, kind='hist') #直方图
hist_ax.set_title('Histogram')
stats.probplot(arma_bic.resid, plot = qq_ax, dist="norm")
sm.graphics.tsa.plot_acf(arma_bic.resid, ax=acf_ax, lags=20) # ACF自相关系数
[ax.set_xlim(0) for ax in [qq_ax, acf_ax]]
sns.despine()

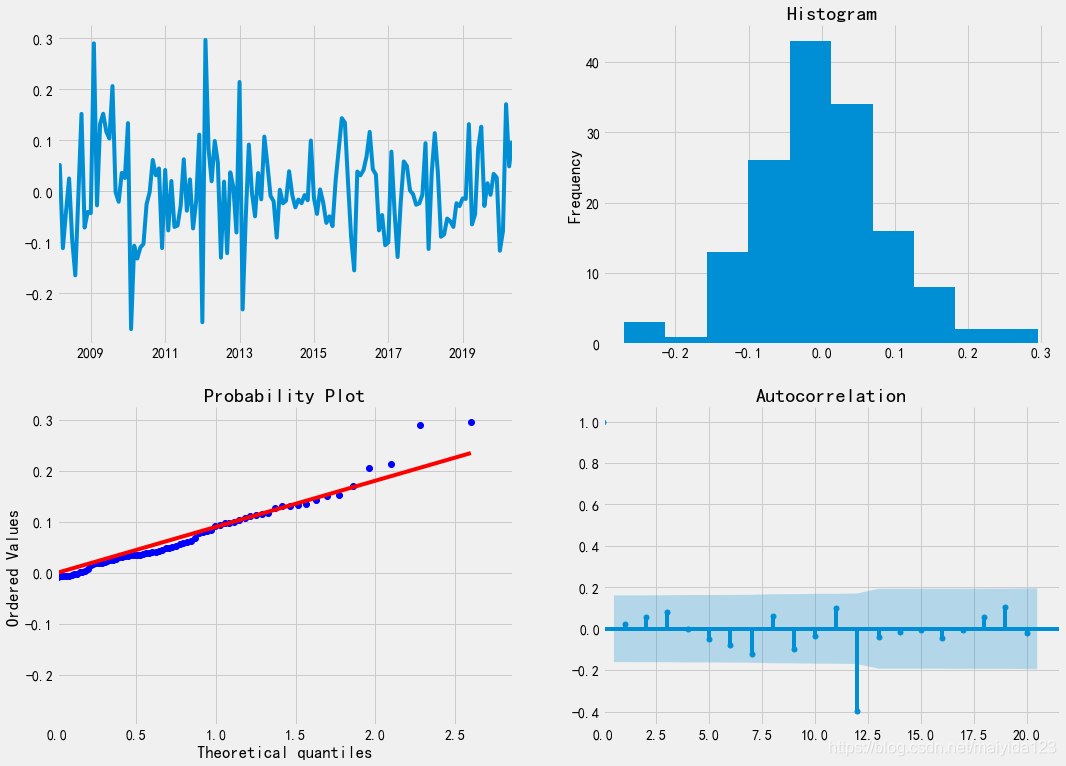
• 残差的时序图较稳定，残差没有随时间出现太大的波动
• 残差基本服从正态分布
• 可以看到残差在前11阶都没有自相关，在12阶处存在自相关。

可见模型的已是一定范围内的最优模型。

3.6 预测

绘制预测图

fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df_train.sales[-36:])
ax.plot(sales_pred_bic, color = 'green', label = 'forecast', alpha=0.7)
ax.plot(sales_pred_bic.index[:12], df_test.values, color = 'yellow', label = 'observed', alpha=0.9)

ax.set_title("ARMA - Forecast of Car Sales")
ax.legend(loc=1)
plt.show()

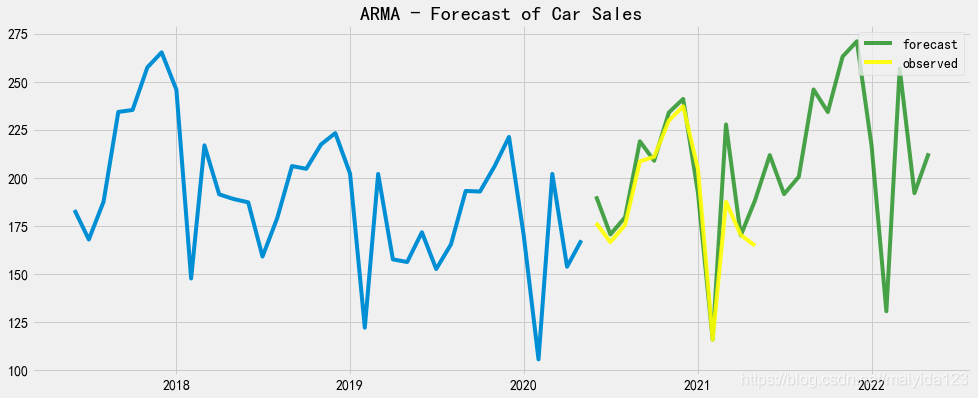
可以看到，汽车销量在未来一年内呈现增长趋势。

4. SARIMAX

在实际使用过程中，我们常常使用网格搜索遍历所有可能的参数，以AIC/BIC统计量最小来选择最优参数，这样做可以简化操作步骤，不需要使用ACF、PACF来确定参数，也能避免主观性带来的偏差。
对于每个参数组合，可以利用SARIMAX()函数拟合一个新的季节性ARIMA模型，并评估其效果。当网格搜索遍历完整个参数环境时，我们可以依据AIC准则从中选取最优参数。

SARIMAX季节性参数：

• endog 观察（自）变量 y
• exog 外部变量
• order 自回归，差分，滑动平均项 (p,d,q)
• seasonal_order 季节因素的自回归，差分，移动平均，周期 (P,D,Q,s)
• trend 趋势，c表示常数，t:线性，ct:常数+线性
• measurement_error 自变量的测量误差，默认False
• time_varying_regression 外部变量是否存在不同的系数，默认False
• mle_regression 是否选择最大似然极大参数估计方法，默认True
• simple_differencing 简单差分，是否使用部分条件极大似然，默认False
• enforce_stationarity 是否在模型种使用强制平稳，默认True
• enforce_invertibility 是否使用移动平均转换，默认True
• hamilton_representation 是否使用汉密尔顿表示，默认False
• concentrate_scale 是否允许标准误偏大，默认False
• trend_offset 是否存在趋势，默认为1
• use_exact_diffuse 是否使用非平稳的初始化，默认False
• **kwargs 接受不定数量的参数，如空间状态矩阵和卡尔曼滤波

如果不指定seasonal_order或者季节性参数都设定为0，那么就是普通的ARIMA模型，exog外部因子没有也可以不用指定； 一般情况下默认参数具有较好的效果。

4.1 网格搜索

%%time
import statsmodels.api as sm
from joblib import Parallel, delayed
import itertools
from tqdm import tqdm

p = d = q = [0, 1, 2]
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in pdq]

def sarima(param, param_seasonal):
    mod = sm.tsa.statespace.SARIMAX(df_train.sales_ln,
                                    order=param,
                                    seasonal_order=param_seasonal)
    res = mod.fit()
    return param, param_seasonal, res
    
# 调用所有核心并发运行，并添加进度条
res_list = Parallel(n_jobs=-1)(delayed(sarima)(i, j) for i in tqdm(pdq) for j in seasonal_pdq)  
data = [[i, j, k.aic] for i, j, k in res_list]  
sarima_res = pd.DataFrame(data, columns=['param', 'param_seasonal', 'aic'])
sarima_res

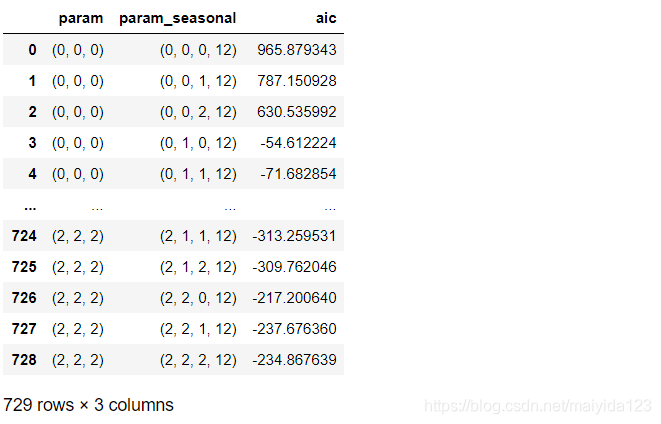
注：我在使用Jupyter运行此代码时会报错：numpy.linalg.LinAlgError: LU decomposition error，换成Pycharm运行或者pdq取值[0, 1]则没有问题。有碰到同样问题的同学可以去statsmodels的issues上找找解决方法，链接：https://github.com/statsmodels/statsmodels/issues/5459 。

查看最优参数

# 查看aic最小值参数
sarima_res.loc[sarima_res.aic == sarima_res.aic.min()]

4.2 建模

best_mod = sm.tsa.statespace.SARIMAX(df_train.sales_ln, 
                                order=(1,1,0), 
                                seasonal_order=(1,0,2,12))
results = best_mod.fit()
print(results.summary())

结果：

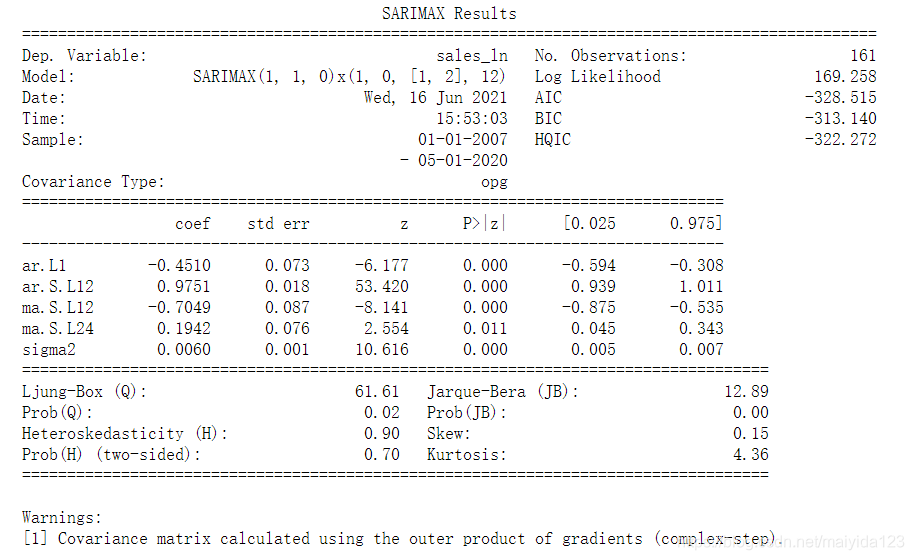
• coef列显示每个变量的权重(即重要性)，以及每个变量如何影响时间序列。
• P>|z|列是对每个变量系数的检验。每个变量的P值均小于0.05，所以在0.05的显著性水平下，拒绝原假设，模型中每个变量的系数通过显著性检验，可以认为拟合的模型中包含这些变量是合理的。

4.3 诊断

# 诊断
results.plot_diagnostics(figsize=(15, 10))
plt.show()

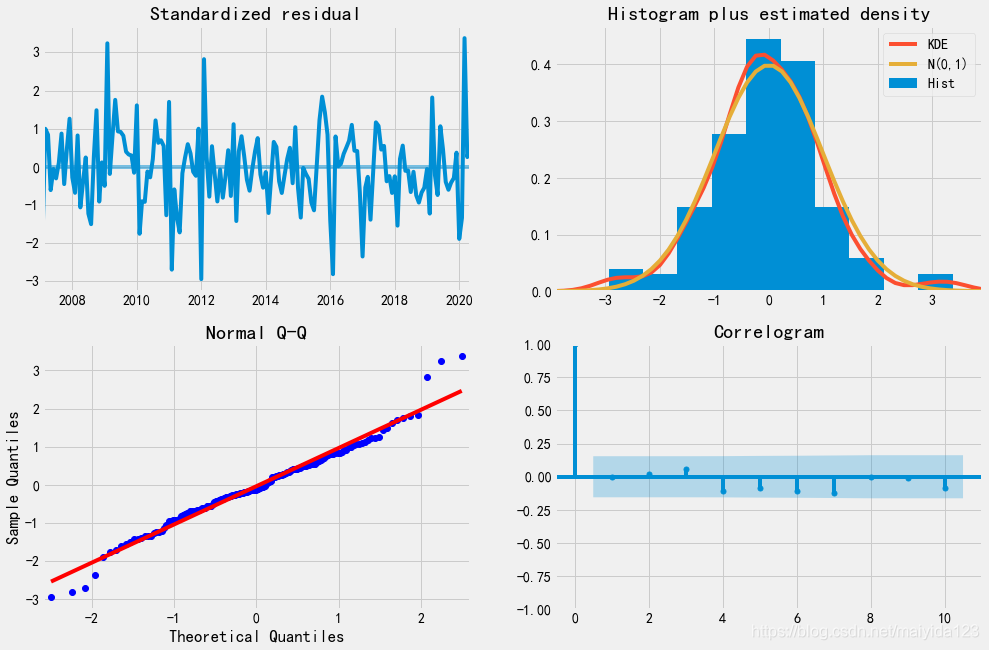
由模型诊断结果可知：

• 观察残差的时序图，可以看到残差基本稳定，随着时间的波动并没有很大的波动。
• 观察正态分布图和QQ图，模型的残差是基本服从正态分布的。
• 观察残差的自相关图，可以看到残差不存在自相关，说明残差序列是白噪声序列。

从残差中不能再提取任何信息。因此可以得出结论，SARIMAX(1, 1, 0)x(1, 0, 2, 12)模型的拟合效果较好。

4.4 评估与预测

# 预测未来24个月的销量
pred_uc = results.get_forecast(steps=24, alpha=0.05)
pred_pr = pred_uc.predicted_mean

# 获取预测的置信区间
pred_ci = pred_uc.conf_int()

# 合并预测值与置信区间
pred_data = pd.concat([np.power(np.e, pred_pr), np.power(np.e, pred_ci)], axis=1).round(2)
pred_data.columns = ['forecast', 'lower_ci_95', 'upper_ci_95']
pred_data

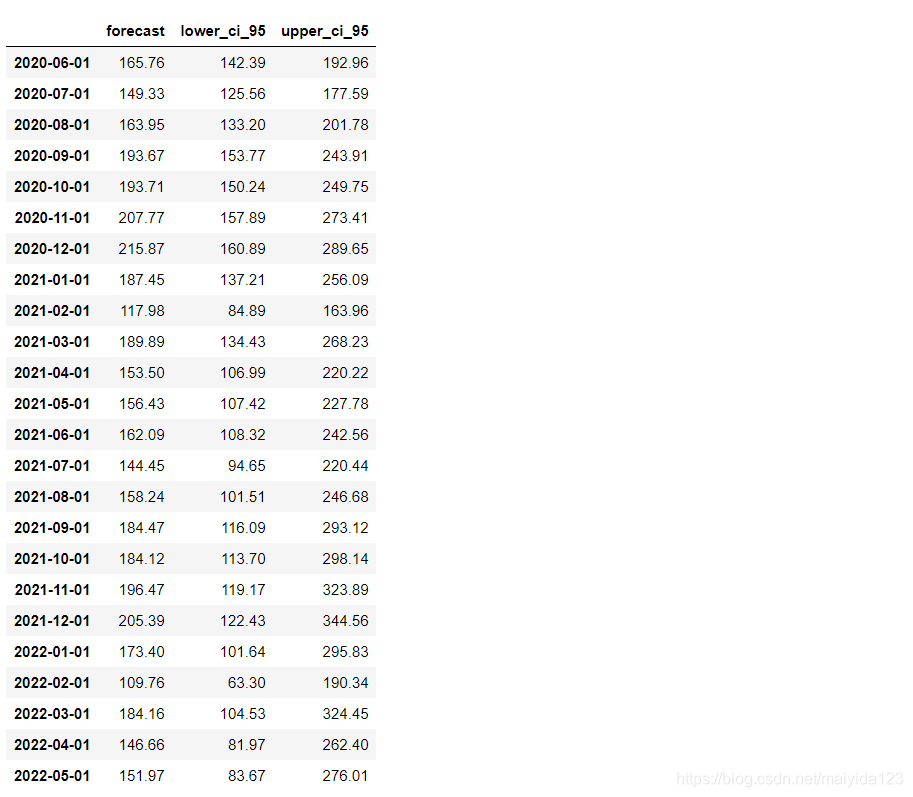
模型评估

# 模型评估---rmse
print('预测值的rmse为 %.2f'%np.sqrt(((pred_data.forecast[:12] - df_test.sales.values) ** 2).mean()))

• 预测值的rmse为 14.83
• 说明预测月销量与真实月销量平均相差14.83w辆

预测时序图

fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df_train.sales[-24:])
ax.plot(pred_data.forecast, color = 'green', label = 'forecast', alpha=0.7)
ax.plot(pred_data.index[:12], df_test.values, color = 'yellow', label = 'observed', alpha=0.7)
ax.fill_between(pred_data.index, 
                 pred_data.lower_ci_95, 
                 pred_data.upper_ci_95, 
                 color='grey', alpha=0.5,label = '95% confidence interval')

ax.set_title("SARIMA - Forecast of Car Sales")
ax.legend()
plt.show()

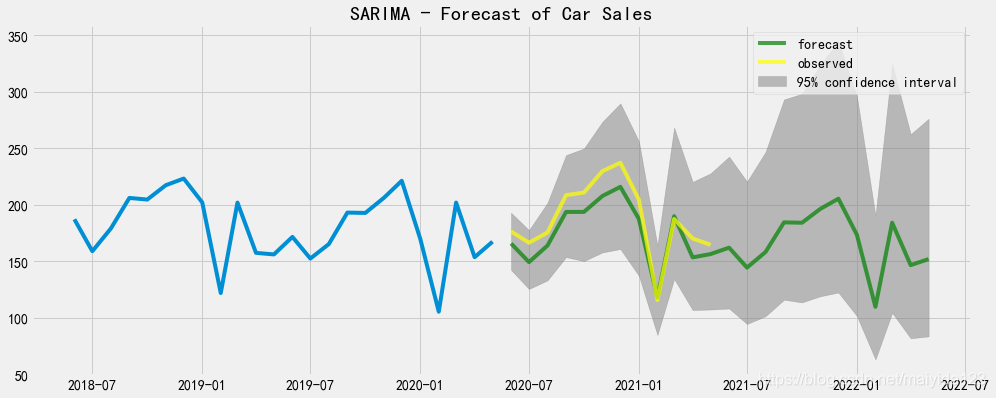
• 可以看到，多数实际值大于预测值，但均落在95%置信区间内。
• 预测未来12个月汽车销量呈下降趋势。

5. Auto ARIMA

Auto ARIMA可以绕过使序列平稳化、定阶等步骤，与SARIMAX相比则无需手动遍历参数，较为方便。其通用步骤：

1. 加载数据：构建模型的第一步为加载数据集。
2. 预处理数据：输入单变量，删除其他列。
3. 拟合Auto ARIMA：在单变量序列上拟合模型。
4. 在验证集上进行预测：对验证集进行预测。
5. 计算RMSE：用验证集上的预测值和实际值检查RMSE值。

常见参数：

1. start_p:p的起始值，自回归(“AR”)模型的阶数(或滞后时间的数量),必须是正整数。
2. start_q:q的初始值，移动平均(MA)模型的阶数。必须是正整数。
3. max_p:p的最大值，必须是大于或等于start_p的正整数。
4. max_q:q的最大值，必须是一个大于start_q的正整数。
5. seasonal:是否适合季节性ARIMA。默认是正确的。注意，如果season为真，而m == 1，则season将设置为False。
6. stationary :时间序列是否平稳，d是否为零。
7. information_criterion：信息准则用于选择最佳的ARIMA模型。(‘aic’，‘bic’，‘hqic’，‘oob’)之一
8. alpha：检验水平的检验显著性，默认0.05
9. test:如果stationary为假且d为None，用来检测平稳性的单位根检验的类型。默认为‘kpss’;可设置为adf
10. n_jobs ：网格搜索中并行拟合的模型数(逐步=False)。默认值是1，-1为使用电脑所有核心。
11. suppress_warnings：statsmodel中可能会抛出许多警告。如果suppress_warnings为真，那么来自ARIMA的所有警告都将被压制
12. error_action:如果由于某种原因无法匹配ARIMA，则可以控制错误处理行为。(warn,raise,ignore,trace)
13. max_d:d的最大值，即非季节差异的最大数量。必须是大于或等于d的正整数。
14. trace:是否打印适合的状态。如果值为False，则不会打印任何调试信息。值为真会打印一些

建模

from statsmodels.tsa.arima_model import ARIMA
import pmdarima as pm

smodel = pm.auto_arima(df_train.sales_ln, start_p=1, start_q=1,
                         test='adf',
                         max_p=3, max_q=3, m=12,
                         start_P=0, seasonal=True,
                         stationary=True,
                         information_criterion='aic',
                         error_action='ignore',  
                         suppress_warnings=True, 
                         stepwise=False)

smodel.summary()

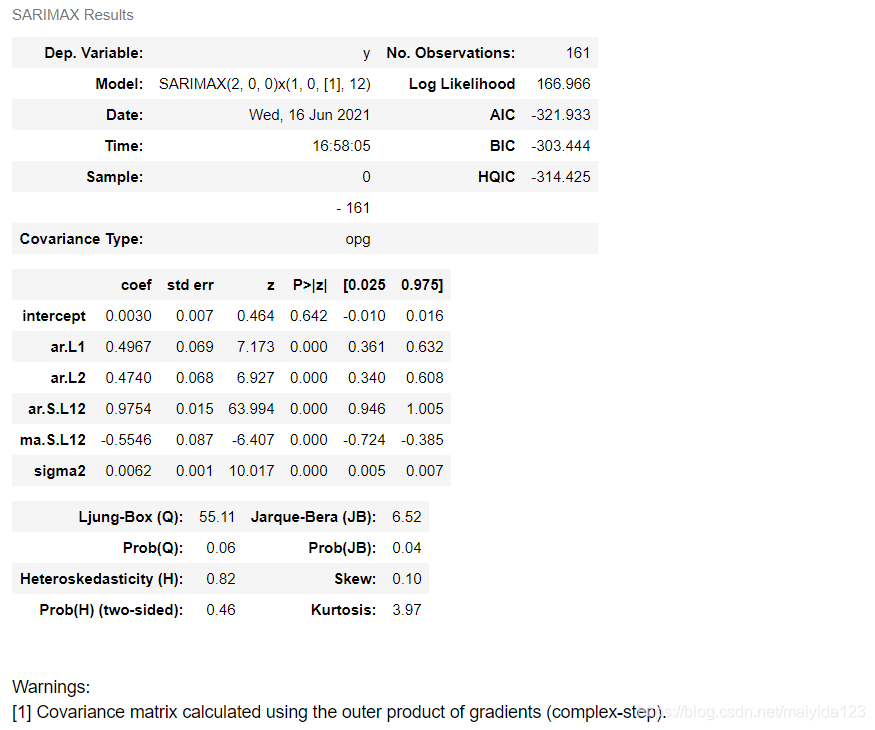
得到的模型为SARIMAX(2, 0, 0)x(1, 0, 1, 12)。

诊断

smodel.plot_diagnostics(figsize=(15, 10))
plt.show()

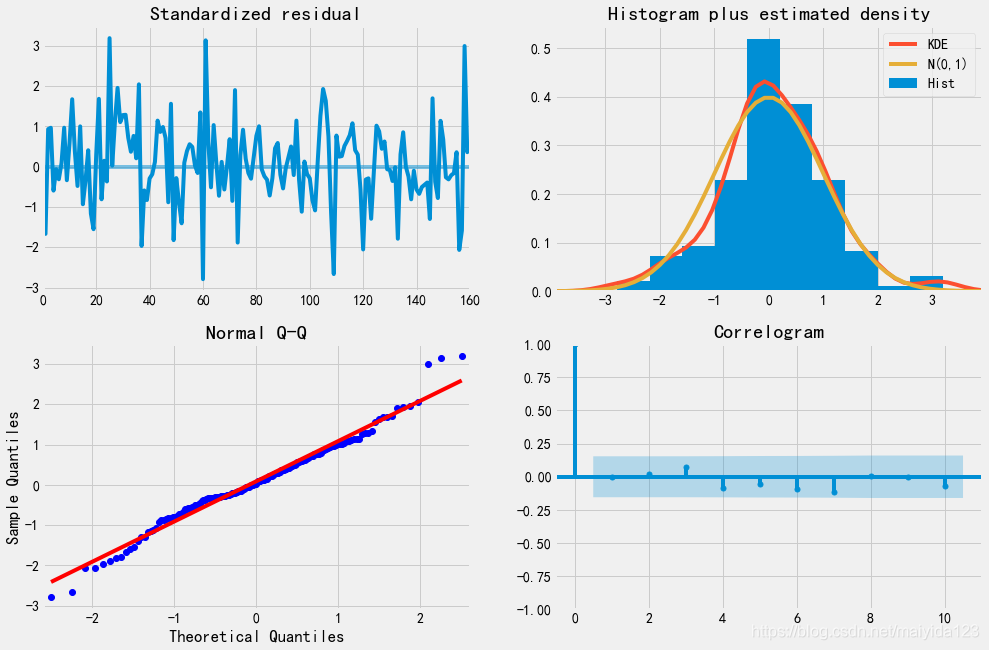
• 残差基本稳定，服从正态分布，为白噪声序列

预测

pred_ln, confint_ln = smodel.predict(n_periods=24, return_conf_int=True)
pred = pd.Series(np.power(np.e, pred_ln), index = pred_data.index)
lower_confint = pd.Series(np.power(np.e, confint_ln[:, 0]), index = pred_data.index)
upper_confint = pd.Series(np.power(np.e, confint_ln[:, 1]), index = pred_data.index)
pred_data_auto = pd.DataFrame([pred, lower_confint, upper_confint], 
                              index = ['forecast', 'lower_ci_95', 'upper_ci_95']).T
pred_data_auto

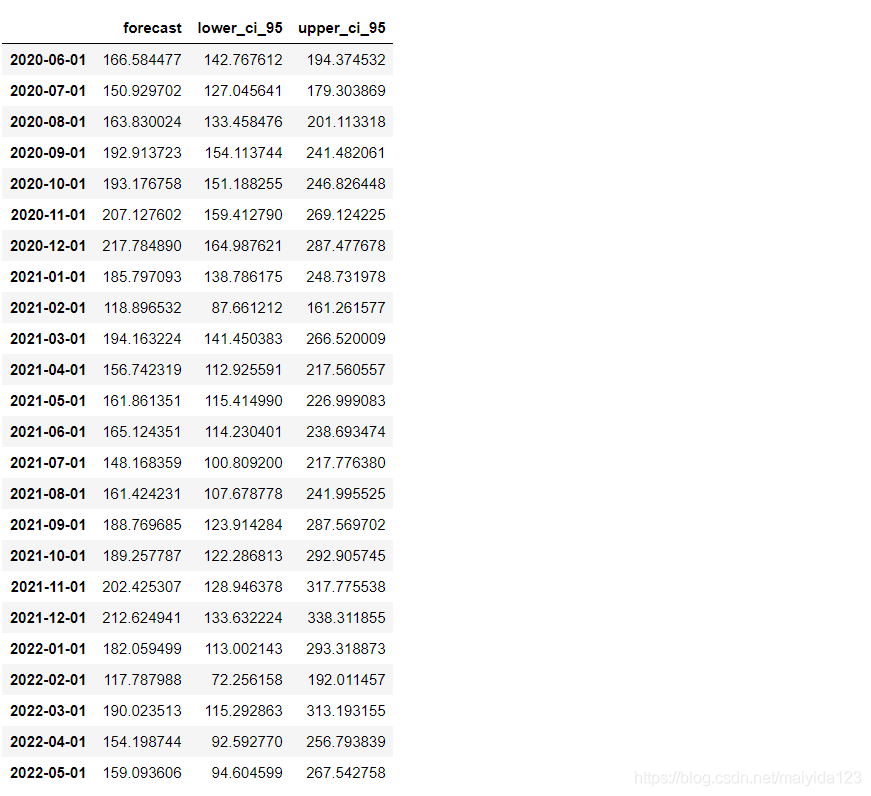
效果评估

print('预测值的rmse为 %.2f'%np.sqrt(((pred_data_auto.forecast[:12] - df_test.sales.values) ** 2).mean()))

• 预测值的rmse为 14.47
• 说明预测月销量与真实月销量平均相差14.47w辆
• 效果比SARIMAX稍好一些

预测时序图

fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df_train.sales[-24:])
ax.plot(pred_data_auto.forecast, color = 'green', label = 'auto arima forecast', alpha=0.7)
ax.plot(pred_data_auto.index[:12], df_test.values, color = 'yellow', label = 'observed', alpha=0.7)
ax.fill_between(pred_data_auto.index, 
                 pred_data_auto.lower_ci_95, 
                 pred_data_auto.upper_ci_95, 
                 color='grey', alpha=0.5,label = '95% confidence interval')

ax.set_title("SARIMA - Auto Arima Forecast of Car Sales")
ax.legend()
plt.show()

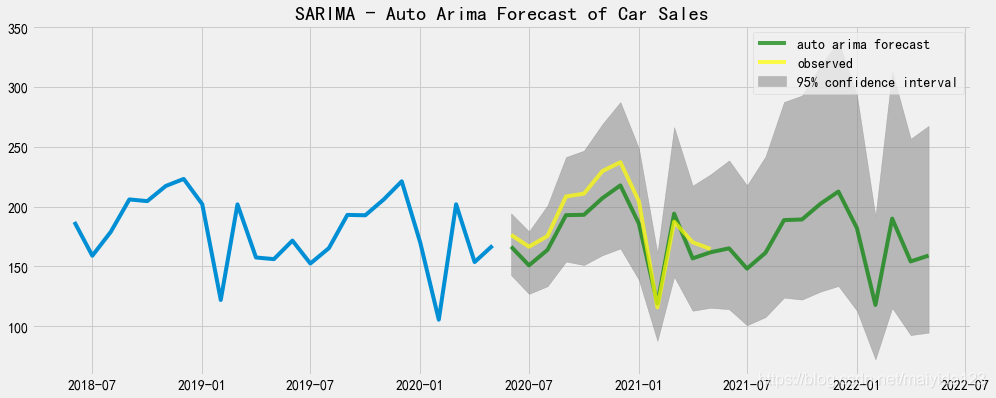
• 可以看到，多数实际值大于预测值，但均落在95%置信区间内。
• 预测未来12个月汽车销量呈下降趋势。

6. 对比与总结

6.1 对比

合并

df_pred = pd.concat([sales_pred_bic, pred_data.forecast, pred_data_auto.forecast], axis=1).round(2)
df_pred.columns = ['ARIMA', 'SARIMAX', 'Auto ARIMA'] 

绘制时序图

fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df[-36:], label = 'Observed')  # 查看近36个月的销量
for i in df_pred.columns:
    ax.plot(df_pred[i], label = i)
ax.set_title("Forecast of Car Sales In The Next 12 Months")
ax.legend()
plt.xticks(rotation=60)
plt.show()

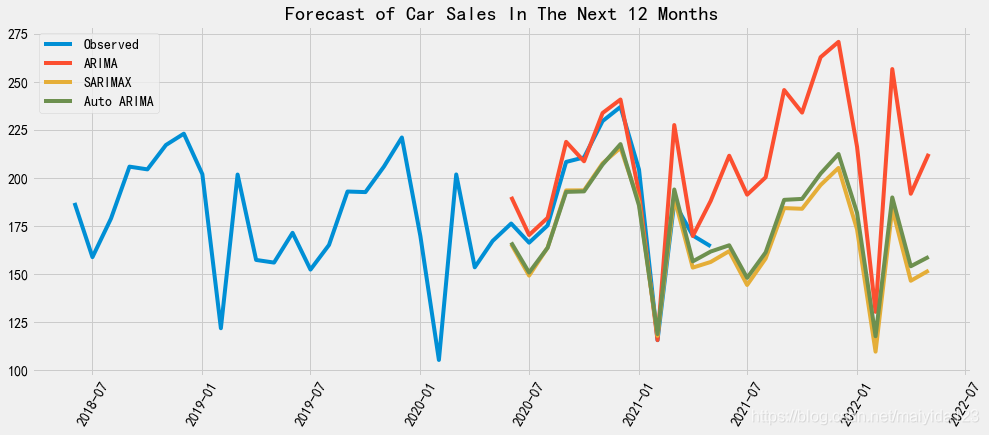
通过对比可以看到，ARIMA预测未来一年销量走高，SARIMAX与Auto ARIMA则预测走低。

df_pred.index = df_pred.index.astype("str")
df_pred = df_pred[12:]
df_pred.append(pd.DataFrame(df_pred.sum(), columns =['合计']).T)

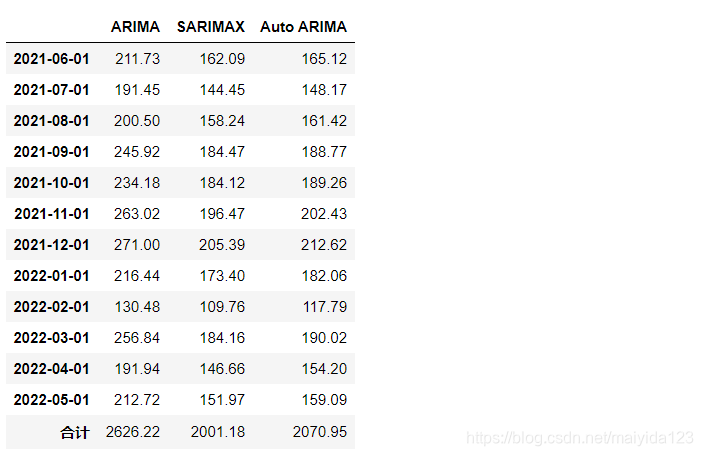
ARIMA、SARIMAX和Auto ARIMA对于未来12个月的汽车预测总销量依次为2626.22、2001.18、2070.95万辆。

6.2 总结

本文分别使用ARIMA、SARIMAX和Auto ARIMA对于过去十几年的月销量进行建模与预测，
1.使用过去一年的销量验证，其RMSE值依次为15、14.83、14.47；
2.预测未来一年的总销量依次为2626.22、2001.18、2070.95万辆；
3.预测未来一年的月销量走势依次为看高、走低、走低。

部分内容参考：
数据分析入门|SARIMA模型案例分析
独家 | 利用Auto ARIMA构建高性能时间序列模型（附Python和R代码）
Python数据科学技术详解与商业实践